「1年を超える期間の―リスクの計算式」で、複数年運用した場合の―リスクの計算方法を解説しました。
複数年運用時のリターン(連続複利)を計算し、上記のリスクの計算式を組み合わせることで、複数年運用後の値動き幅を計算することができます。では、どうやって、計算するのでしょうか?
(1)複数年運用時の期待リターン(連続複利)を求め、複数年運用時のリスク分を加えます。(2)そして、計算結果の期待リターン(連続複利)を、期待リターン(年複利)に変換します。上記2つの計算式を、具体的に解説していきましょう。(1)の計算式は、ln(1+期待リターン)×想定運用年数±リスク×想定運用年数 です。*(2)の計算式は、exp(連続複利のリターン)-1 です。
図:複数年運用後の値動き幅の計算式
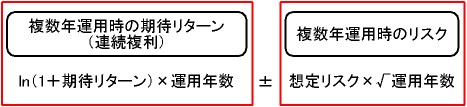
※ 複数年運用時の期待リターン(連続複利)の計算内― ln(1+期待リターン) は、"期待リターン(年複利)"を"期待リターン(連続複利)"に変換する計算式です。
※ 複数年運用時の期待リスクの計算については、こちらを参照→1年を超える期間の―リスクの計算式
以下の計算例は、"リターン10%・リスク20%の投資商品に、5年間投資した場合"―という前提で計算したものです。
ln(1+0.1)×5±0.2×√5=0.48±0.45
最も良かった場合:期待リターン(連続複利)+リスク=0.93(連続複利)
→年複利に変換:exp(0.93)-1=1.53(年複利) +153%
最も悪かった場合:期待リターン(連続複利)-リスク=0.03(連続複利)
→年複利に変換:exp(0.03)-1=0.03(年複利) +3%
- なお、この記事内の"複数年運用時のリスク"は、"1標準偏差"で計算しています。1標準偏差の特徴は、以下です。約68%の確率で、上記の結果になります。残りの約32%の確率で、記事内の想定よりも、"上回る"か"下回ります"。(確率は、半分の約16%ずつ)
わき道にそれますが、googleの検索窓に、計算式を入力しても計算できます。(ln・expも計算できます。)